Kezdő útmutató a bináris fákhoz

Ha elvégezte az adatstruktúra tanfolyamot informatika szakán, vagy autodidakta programozó, akkor valószínűleg találkozott a „Bináris fák” kifejezéssel. Bár kissé lehengerlőnek és bonyolultnak tűnhetnek, a bináris fa fogalma meglehetősen egyszerű.

Olvassa el, amikor bináris fákat boncolunk, és miért szükségesek a programozók számára.

Mik azok a bináris fák?

A bináris fák az egyik első adatstruktúra közé tartoznak, amelyet a diákok egy adatszerkezeti tanfolyamon tanítanak. A bináris fa sok csomópontból áll, és a bináris fa minden csomópontja két mutatót tartalmaz, amelyek a bal és jobb gyermek adatcsomópontokat jelzik.

A bináris fa első csomópontját gyökérnek nevezik. A fa utolsó szintjének csomópontjait leveleknek nevezzük.

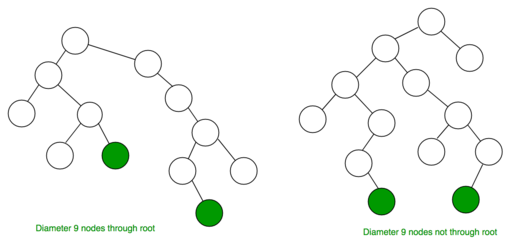
Minden csomópont tartalmaz egy adatelemet és két csomópont -mutatót. Az üres bináris fát nullmutató jelzi. Amint már rájött, a bináris fáknak csak két gyermekük lehet (innen a név).

A bináris fa szerkezetek típusai

A csomópontok elhelyezésének módjától függően több különböző bináris fa szerkezet létezik. A bináris fát teljes bináris fának nevezzük, ha a fa minden csomópontja nulla vagy két gyermekkel rendelkezik. Egy tökéletes bináris fában minden csomópontnak két gyermeke van, és a levelek ugyanolyan mélységben vannak.

Összefüggő: A legjobb módszerek az ingyenes kódolás megtanulására

Egy komplett bináris fa minden szinten csomópontot tartalmaz, kivéve az utolsó szintet. A teljes bináris fákban a csomópontok a gyökér bal oldalán koncentrálódnak. Egy másik gyakori szerkezet a kiegyensúlyozott bináris fa; ebben a struktúrában a jobb és a bal részfa magassága legfeljebb eggyel eltérhet. Szükséges továbbá, hogy a bal és a jobb részfák is kiegyensúlyozottak legyenek.

Fontos megjegyezni, hogy a kiegyensúlyozott bináris fa magassága O (logn), ahol n a fa csomópontjainak száma.

Bizonyos esetekben, ha minden csomópontnak csak egy bal vagy jobb gyermeke van, akkor a bináris fa ferde bináris fává válhat. Ekkor úgy fog viselkedni, mint egy linkelt lista, az ilyen fákat degenerált fának is nevezik.

Mik azok a bináris keresési fák?

A bináris keresési fa (BST) lényegében egy rendezett bináris fa, amelynek különleges tulajdonsága a "bináris keresési fa" tulajdonság. A BST tulajdonság azt jelenti, hogy a gyökérnél kisebb kulcsértékű csomópontok a bal részfába kerülnek, és a gyökernél nagyobb kulcsértékű csomópontok a jobb oldali fa részei.

A BST tulajdonságnak igaznak kell lennie a fa minden következő szülőcsomópontjára.

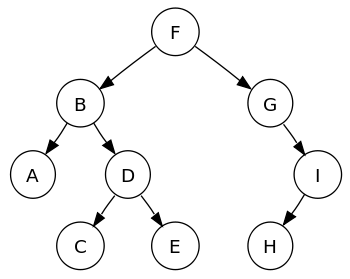
A bináris keresőfák gyors beillesztést és keresést kínálnak. A beillesztési, törlési és keresési műveletek legrosszabb esetben O (n) bonyolultságúak, ami hasonló a linkelt listához.

A bináris fák előnyei

A bináris fák számos előnnyel járnak, ezért továbbra is nagyon hasznos adatstruktúrák. Segítségükkel a szerkezeti kapcsolatok és hierarchiák láthatók egy adathalmazban. Ennél is fontosabb, hogy a bináris fák hatékony keresést, törlést és beillesztést tesznek lehetővé.

A bináris fa megvalósítása és karbantartása is nagyon egyszerű. A bináris fa a programozóknak a rendezett tömb és a linkelt lista előnyeit kínálja; a bináris fában való keresés olyan gyors, mint egy rendezett tömbben, és a beszúrási vagy törlési műveletek ugyanolyan hatékonyak, mint a linkelt listákban.

A bináris fák fontos adatstruktúrák

A bináris fák nagyon fontos adatstruktúrák, és elengedhetetlen, hogy a programozók kényelmesen alkalmazzák őket programjaikban. Az interjúztatók gyakran olyan egyszerű bináris fa problémákat kérdeznek, mint a bejárások, a maximális mélység, a tükrözés stb.

Javasoljuk, hogy ismerje meg a bináris fa fogalmát, és ismerje meg a tipikus interjúproblémákat.

TreeViz: Egyszerű módszer az adatstruktúrák vizualizálására

Olvassa tovább

A szerzőről